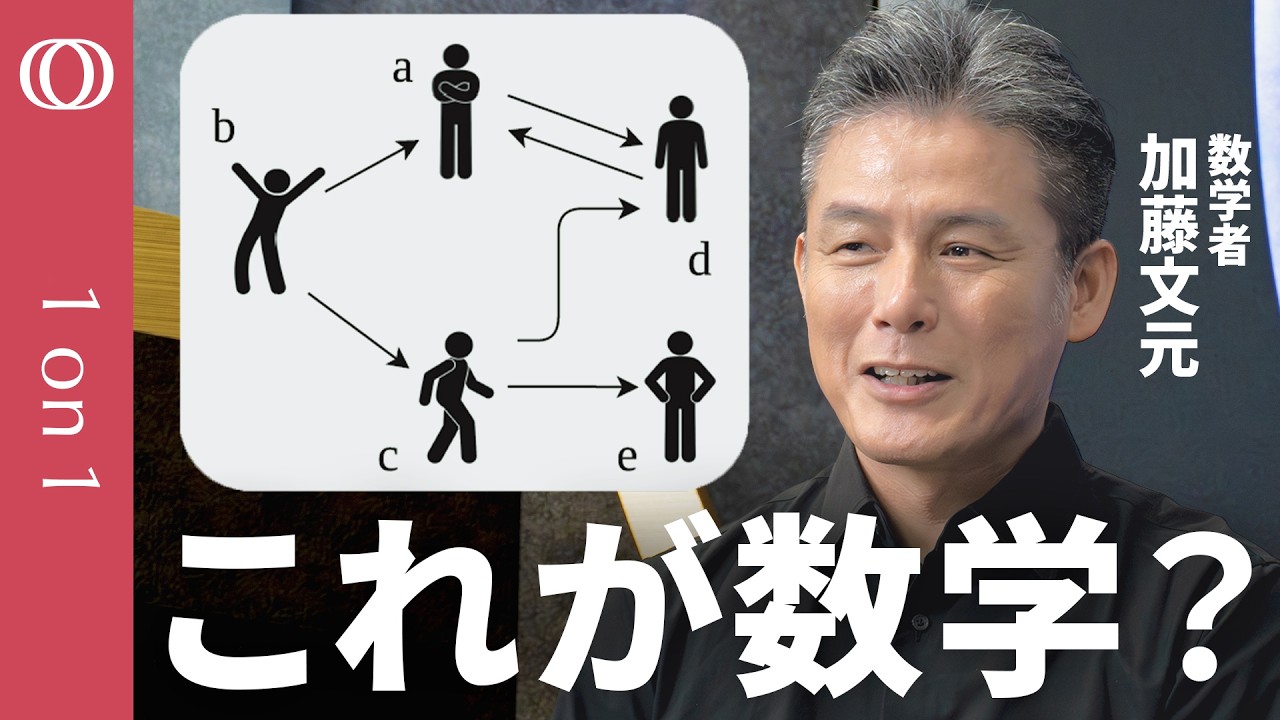
【ほぼハンバーグで数学「圏論」を語ります】数学者・加藤文元／関係性に注目し必要な物事を浮かび上がらせる／「部署と社長の間に調整役が必要だ」／マスターしたらカルボナーラの作り方を数式で描ける【1on1】

【ほぼハンバーグで数学「圏論」を語ります】数学者・加藤文元／関係性に注目し必要な物事を浮かび上がらせる／「部署と社長の間に調整役が必要だ」／マスターしたらカルボナーラの作り方を数式で描ける【1on1】

これ、あの、カルボナーアーラの作り方ちょっと意外に思うかもしれないんですけど、これ実は数式なんですよ。 [音楽] これが数式なんです。これ、これが数式なんです。権論の専門的な言葉で言うと、対象物だる剣の中におけるストリング図式っていう書き方。この権論の言葉をマスターすればちょっと待って。 それ役職じゃなくて食でいいんじゃないとかっていうみんながその精密な関係の関係の関係の話を今してるんだなみたいなそういうコミュニケーションが取れるようになるかも。クロスリーグ [音楽] 1始まります。3 セリターの鈴木です。私は去年まで NHK者をやっておりまして科学を担当しておりました。あのクロスでも科学の分野を届けていきたいという風に思っております。 で、今日のテーマはですね、社会の見る目 を強化する数学論です。まずはちょっと こちらをご覧ください。あの、こちらです ね、あの、記号が矢印で繋がれてるのが 分かると思うんですけども、これが権論な んです。で、これ一般な数学なんですけど も、ま、この見方を使うと実は カルボナーラの作り方がこのようにかける ということです。 で、このようにですね、生活においてもですね、新たな視点を得ることができるという権論なので、ま、こちらについて今日は詳しく聞いていきたいという風に考えております。ゲストを紹介します。え、全大学教授で数学者の加藤ふさんです。よろしくお願いします。 よろしくお願いします。 で、先生ですね、あの、この 10 月に、あの、初めての権論という本を出版されたということで、ま、こちら、あの、まずです、その数論企画が専門の先生か、これなぜこうやって、あの、一般者向けのですね、この権論書こうと思ったのかってのはどういうことなんでしょう? ま、権論ってこれあの数学の世界ではかなりこう、ま、ここ数十年で革命的な こういろんなあの、ま、近く変動をね、や起こしていてで、ま、強力 その表現ツールでもありながらこう新しい考え方をどんどんこう出す 数学の中で生み出すみたいなね。 そういうものになっていてでさらに最近もう数学をさらにの枠を超えてね、 ま、いろんなところに公用されるようになったんですね。自分は最初数学の はい。え、1 つのツールとしてね、あの、仕事のために使ったりするために学んできたわけですが、あの、走行してるうちに、いや、これすごくないって思って、これもっとあの、 なるほど。 みんなにその世界のみんなにこの権論をはい。あの、伝えたいみたいなはい。そういう感じでした。 本ん当に数学の世界だけじゃなくて本当いろんな世界でも使えるようになってきてるので是非これを知っといて欲しいというところで。 そうですね。 ね、これ、あの、カルボナーラの作り方ってちょっとやってみた。やってみたんけど、あの、ちょっと意外に思うかもしれないんですけど、これ実は数式なんですよ。 これが数式なんです。 え、これ、これが数式なんですよ。あの、 あの、権論の、ま、こう専門的な言葉で言うと対象物だる剣っていうあの件の中におけるストリング図式っていう、 そういう書き方で書いたものなのね。 ただ数字も記号もないように見受けられるんですけども。 え、まあまあ、あの、スパゲッティとかっていう記号がある。あれ記号なんで で、茹でるとかっていうのも、ま、希望で あります。はい。あと、ま、黒い丸はありますね。 あ、あれ捨てなさいっていう意味ですね。茹で汁捨てるとかだから多分あの通りに作ったら美味しいものできないと思うんですけど。 茹で汁ば使わなきゃいけないんですので。 そういうやつ、ま、ああいう感じのね。 はい。 あの、要するにカルボナーラのレシピが数式でかけちゃうみたいな。 そういうあのものなんですよね。 わかりました。じゃ、今日はですね、あの 3 つのテーマであのお伺いしていきたいと思います。まあ 1 つ目はですね、権論とは何かというところで、ま、あの権論はですね、あの先ほど見たように関係の関係また関係というものを論じるつけだということで、ま、まずこちらを聞いていきたいと思います。で、 2 番目に論の税材、あの、監守自然変換っていうことで、あの、論における要な 概念をですね、学べたいという風に思います。 で、3つ目、あの、こちら権論が開く世界 の新しい景色と言いますけども、こちら、 あの、まさに先ほどのカルボラの付け方の ようにですね、あの、権論が私の生活、 仕事にどう応用できるのかっていうことを 聞いていきたいという風に思います。で、 まずと何かからお伺いしていきたいんです けども、あの、先生の著所を読んで ちょっと驚いたのが最初にあの、モナカと マカロンの関係が出てくるんですね。 こちら説明していただいてもいいですか? はい。 で、これ、あの、いや、皆さん知ってますよね。みたいな。あの、えっと、何でしたっけ?以前 何年か前、56年前だと思うんだけど、 あの、ミルクボーイのネタです。あの、モナカ モナカの家計図知ってるっていう、あの、あれですよね。で、それで、あの、あの、ネタを読んでけ書いてみたっていう、 そういうものなんですけど、これあれですね、それをもう権論的視点で見てらっしゃるってことなんですね。 そう。だ、剣として見てます。はい。だ、モナの剣なんです。 これね、 それだからこうモナカとかモナ王とかっていうのがその剣の中におけるもなんですね。 物っていうか対象ってあ、言いますけど で、あの、そいつらがその矢印で繋がってます。ま、残念ながらその、 え、ミルクボーイさんは、 あの、モナのその親は誰だって言ってないので、ま、ちょっとただの白丸になってるんですけど、こう生八橋っていうのは兄弟だとかね、 もみまじは従になってるんですよね。 で、あの、マカロンは、あの、モナのその子孫になってて、何台先の子孫かって言ってないので、しょうがないので、てんてんてんて、あの、ちょっとお茶濁してるんですけど、そういうやつです。 また本を読むとですね、これモナじゃなくと、ま、違うものが出てくるんですよね。 これが手巻き寿司とクレープと、 あ、ええ、こので、こちらはなんでこう書かれたのかとか、 え、いや、これあの、出なくって私が適当に、あ、私のネタです、これは。はい。なるほど。 はい。手巻き寿司っていうのが、ま、モナ中みたいな はい。 人がいてで、あのサバの寿司ですね。 はい。 で、あの稲寿司はなんとなく糸いこっぽいなみたいな。 ま、確かにそうですね。ちょっと形違いますね。 ええ。で、モナとモナカの関係だったら、 ま、手巻きとカリフォルニアロールかなみたいな。 なるほど。 ええ、で、あとマカロンが子孫だったわけですなか。モナカの場合はクレープっぽいなっていう。 はい。はい。 で、これなぜこのモナカとそのマカロンの関係、そして手巻き寿司とクレープの関係を こう考えるでしょうか?それともなんかこ いや、それね、そのなんて言うんですかね。だからその手巻き寿司とクレープの関係って今言ったようになんかこうモナカとマカロンの関係 にちょっと似てるような気がするじゃないですか。はい。ま、確かにそうですね。はい。 ええ。で、あのなんて言うんですかね?手巻き寿司とモナカが似てるって言ったら はい。 誰もあの何それって思うと思うんですよね。似てないです。 何言ってんですか?みたいな。 で、クレープとマカロン似てるねって言っても多分へふなんかみんな首をかしげると思うんですよね。 だけどその はい。 え、モナカとマカロンの関係とは 手巻き寿司とクレープの関係に似てるっていうその関係が似てるっていうのは なるほど。 あ、そうかもしんないみたいな。 はい。 でね、結構人間って その、 今僕そのモナと手巻き寿司が似てるって言ったら何言ってるのって言われるようにね、 こう物ともが似てるってあんまりないんですよ。 普通は物ともって似てないんですよ。 だけど我々が例えばこう世の中を見て あの、ま、色々こう水量をしたりとかいろんなこう推理をしたりする時ってこう何と何は似てるぞうんとかって考え始めますよね。 それって大抵は関係が似てるからなんですよ。 あ、そうなんですね。 そう、 そうか。ま、物が違う。もちろん名前が違うので。 そう、そう、そう。 ま、確かに似てる、似てないから名前をつけて区別してるわけですけども うん。うん。 確かに誰、誰が似ているっていうのは うん。 何かその例えば顔が似てるとかでもその目、目と鼻の関係が似ているのかとか、配置が似てるのかとか。あ、そういうこと。 [音楽] あるいはなんかこう人間関係があそこの関係はそこの関係に似てるとかってよく話題にするじゃないですか。 そうですね。 あの上司と部下の関係とあの似てそういうそういうやつそういうやつで結構だからそういうこう関係に我々結構注目するんですよね。 ははは。 で、あの、やはり特に数学なんかはこう、やっぱりロジックの、え、 [音楽] 学問なので、そう、こう、そういうな論理的な水なんかね、推理をするんですけど、 こう権論っていうのはそういうなんか こう関係が似てますねみたいなそういうのって、ま、いいわゆるアナロジーって言ったり、あるいはこうメタファーって言ったり、こう例え、例えですよね。勇 そう、そういうものにこうね指してるっていうか、そういうものを表現する力を持ってるわけです。 なるほど。 え、1 つ上のくらいというか、少し俯瞰してみた時のあの景色というか。え、え、ええ。 普段でもそういうのって我々は 無意識にそういうのこう言語化してるんだけどあんまりそれを言葉にはっきりと言わないじゃないですか。はい。 でも論はそういう言葉をこうなんですかね、たくさんくれるわけです。まさにそのあまり喋らないとその多分言葉がないというか、あのそれをそうです。表現するものがない。そう、そう、そう。 わけですけども、 実はすぐにはそれがあったという。 そう、そう、そう。こう縦の線は剣の中でのね、あの車っていう はい。 矢印なんですけど、横のうん。あ、車っていうのはね、 あのなんです、 映すとか。あ、です のやつですね。こう弓をるの。うん。 はい。 なんだけど横の線はこれ監守って、ま、後でちょっと説明しますけど いう、ま、ちょっとワンランク上の関係を表す矢印なんですね。 なるほど。 で、実は権論にはさらにそのワンランク上もあるですということなんです。 分かりました。 検論の概念が分かってきたところで次のテーマと言っていきます。あの権論の親はその県監守自然変換ということで、ま、この 3つが1 つ重要な概念になってくるということなんですね。ちょっと難しいことからお伺いしていきたいんですが、まずこちら今出ているのは件の定義ですね。 こちらちょっと説明していただいて。 はい。基本的には、まあ、 1番その2 行目ぐらい見るとこ対象の集まりってあるじゃないですか。 ありますね。はい。 だからなんかこう物がまずあります。物の集まりがまずありますっていう。はい。 で、それを次の行がそのもともがあったらね、ま、 AとかB と書いてあるのがあれ物なんですけど、その AからB にこう矢印っていうもう感じが書いてると思うんですが、っていう それの集まりっていうのを考えましょう。それはだから AとBを ま、こう方向がついてるわけですけど、関係を表すシンボルなんですね。 だ、これがる対象というのは、ま、まさに物さ言えばモナカみたいなでというのは先ほどのモナからモへのその何印がありましたけども、ま、もともを繋いでる関係性みたいなものを 表してると表 してると。ま、それがだけど関係性はもしかしたら 1 個だけじゃないかもしれなくってこういろんな関係があり、なんかこう 100 個関係があるとか、ま、場合によっては全然関係がないっていう。 そういう場合は、あの、集まりって言ってもあのその要素は 0個っていう 空習になるわけですね。 うん。 でもそういうそれがなんかいくつかあの、ま、条件を満たしているとかっていう、ま、それが、ま、 1番重要な条件は 1番最後のあのかこB って書いてる条件なんですけど、あ、その前にだから、 えっと、1番、丸の4番目か、丸の4 番目が大事なんだけど、その矢印って合成できるっていう はい。 うん。これ意味はわかんないでしょ? そうですね。さっきのモナ中で言ってもちょっとわかんなかったですね、今。はい。 矢印をするってなんか物の変化だとかあるは物になんか物がこう何かの動作をするっていう思ってもよくって例えばあの まスタを茹でるっていう はいはいパスタ そうと はい それからあのそのその前にパスタを測るっていう操作をまあじゃないですか 1人ええ1人頭まgとかいうでしょ それだから測って茹でるっていうのをま その2 つを合成したら測って茹でるっていうのを 1つの操作と思うっていう なるほど。 そういうその合成っていうのがあります。 はい。 うん。そこがだから なるほど。ただそれは全部県の中に入ってるなんですね。 そう。県の情報としてそういうのが入ってるっていう。 ええ、ていう、ま、そのぐらいま、抑えとけば もう問題かなと。 大体大体よろしいんじゃないかと思います。はい。 このハンバーグに考えると件が分かりやすいというところで、 えっと、ハンバーグの件をですね、あの、先生に持ってきていただきました。 こう、あの、ハンバーグの件とかで論の本書く人って、あの、多分史場初だと思いそうですよね。他のちょっとちょっと見てみましたけど、ちょっと見たことないです。 [音楽] あの、それでも、ま、あの、ふざけてるわけじゃないんですよ。あの、大真面目で書いてるんですけど、 その、ま、例えばこういう今こう見てもらうとですね、 大体その、1番その 左上にハンバーグっていう巣のハンバーグがあるわけですね。 はい。あ、もうそのまま先ほどの絵にもありましたけど、ま、焼いただけの 鬼があると。 はい。 だけどその矢印ってのは大体こそれに何でもいいから 1と加えるみたいな そういう風に思ってください。例えばこうソースデメグラスソースをかけるとか あるいはトマトソースをかけるとかちょっと和風にアレンジしてみるか。 ま、あるいはあのチーズ乗せるっていうのもありますね。 だからハンバーグの真下にチーズハンバーグってありますけど、あれ、あの矢印はあれチーズ乗せるっていう意味です。も、そういう矢印色々種類があって 例えばチーズを乗せてデミーグラスソースをかけるってなるとデミーグラスチーズハンバーグになるわけです。 はい。 で、あの、それっていうのは実はチーズを乗せる前にデミーグラスソースかけてもいいんですよ。 そうですね。 ま、ちょっとなんか見栄え違うわけですけど、デミグラスソースをかけてからチーズを乗せるっていう。 それでもデミグラスチーズハンバーグになるっていう。ま、ちょっと苦しいんですけど。 [音楽] うん。 そのでそれからさらにデミグラスソースをかけて煮込むとかね。は、 そうするとデミグラス煮込みハンバーグになるとかっていう。 あ、 はい。ただあれですね、さっきおっしゃったようにその合成ができるのでチーズを行ってからデミグラス行くのとデミラスかけてからチーズ行くのでは うん。はい。 同じ矢印が同じところに最後焼きついてるとこれは合成されていて 同じ矢印と見込めるというところなんですね。 はい。え、大体そのこうミレスとかに行ってハンバーグのケージを見るとそれらの間にこう無意識のうちにみんなこう矢印で結んでると思うんですよね。 あ、これになんかこう 1つま加えたのがこれだなみたいな。 はいはいはいはい。 うん。 で、車があると車があった行き先の方が少し値段が高くなってるわけです。 普通はだからチーズハンバーグの方がハンバーグ力安かったりしたらどうしてと思うわけですよね。そういうこと普通ないわけです。 だ、そういうなんか 無意識にそういうなんか件みたいな構造を実はあの 1 ページの中でこう我々は見てるんですよ。 ま、ちょっといい加減なんですけども、 ま、普通はもうちょっとあの数学の言葉で件を あ、する 記んですけど、あの数学知らなくても読める本っていうの目指したので、こういう感じになったってことですね。 なるほど。はい。 ま、先ほ、あの、見たそのの定義は少し難しかったですけども、ま、こういう風に考えればいいとこ、え、もがあって矢印があるっていうことの意味は分かってもらえるんじゃないかなと思います。 分かりました。 はい。 では次に件が分かってきたところで監修。 あ、監守って多分だから純前とある造語合語だと思うんですよね。 ま、あの、え、英語だとファンクターって言って、これもよくわかんない言葉なんですけど、これは 2つの件の間の、 ま、剣ですからもその剣の中身の中でたくさん物があって矢印があるわけですけど、そのそれを 1個のユニットだと思ってそれを 2つ用意するわけですよね。で、その 2つの件の間の関係っていうのを、 あの、監守と言います。 で、ま、大体だからその、ま、抑えて欲しいのはこう上の丸 2つあるんですけど、 あ、上2つ両方ともってことです。 ええ、1つは物から物へ対応する矢印。 はい。 うん。だからその、ま、 Cっていう件と Dっていう件があるんだけど、 Cのものに対してこう対応する。 それはDの何かもが対応するっていう。 さと手巻き寿みたいなそういうことですね。うん。 物の対応ですね。 はい。 で、それだけじゃなくって次の丸はその関係も対応するっていう うん。ふんふん。 だからAとBの間に関係があったら はい。 そのAとBの行き先、 それFA、FB って書いてるんだけど、その間の関係が対応してるっていう。 なるほど。 矢印が対応するっていうことですね。 で、 最初ので言うと、モナカマカロンのこの矢印 と、そう、 手巻き寿司クレープのこの矢印矢印ですね。はい。なるほど。 まさ、まさにそういうあのことをこう意図して作られるものなんですね。ほ ものだけじゃなくって関係に対しても関係付けようっていう なるほど。 ええ、 これが監守という監守 ものです。ますね。 はい。 実はその冒頭に見たこれこちらも監修なんですね。 一応そのつもりで で左側、ま、あの、冒頭におっしゃっていただきましたの左の丸がもう 1つの剣を表していて、右の丸も 1つの剣を表していて、それを Fという監視で今繋がっていると。 そうですね。だから例えばあの左側の丸の中に Aっていう1番真ん中ぐらいに小文字の Aって書いてますよね。あの、A っていうものは右の丸の中では F括A っていうところに対応してるわけですね。それはだから物が物に対応してる。同じように BっていうのはFBに はい。はい。 Cっていうのは小文字のC ですけど、それはF括この小文字の Cっていうやつに対応してる。 で、それだけじゃなくって、例えばその左側の丸の中で AとBが1 個矢印で繋がってますよね。繋 AからBに行く矢印。 はい。で、小のFがあ、 そうですね。その小文字のF が書いてますね。 それ矢印の名前がついてそれ F っていう名前なんだけど、それがまたラージ Fで、お文字のFで、その小文字のF っていう矢印自体がまた矢印に対応するわけです。 それはF括AからF括Bへの矢印っていう AさんとBさんの関係が FAさんとFBさんの関係に 対応するっていう ことですね。 分かりづらいですね。 そうですね。 なのでこれもちょっとハンバーグで 考えていきたいという風に思います。 なるほど。 で、こちらが先ほど見たハンバーグの剣ってことで、これは 1つのハンバーグ、ま、先ほど図で言うと 1 つの丸の中、中身を表しているわけですけども、 だ、こちらにの、え、を、こちらを監州を使ってた例というのがこちらライスセット監ということで、 こちらもそしてちょっと説明いただいて。 えっとですね、あの監証なんですけど、ファミレスなんかに行ってハンバーグのページを見ると下の方に あのライスセットとかセット書いてあるじゃないですか。あれ [音楽] メニューじゃないですよね。 あ、メニューじゃないですね。確かに。あの、その例えばハンバーグとかそのチキンとかじゃないです。 あれ、あれ、あれを単品でライスセット単品で注文するっていうことは不可能ですよね。 そうですね。はい。 あれだけど同じページに書いてるわけです。 はい。 だ、そこに書いてあるかこういうものとして実は概念としてはハンバーグのメニューとは違うものとしてそこに書いてあるわけ。 確かに あれ実はだから監守なんですよ。 あれ監守なんですか? 監守なんですよ。あそこ書いてるの。だからそのこれから監守って何かと思ったらそのメニューファミレスのメニュー鏡の下の方に書いてるやつだっていう思ってくれれば大体いいんじゃないかなと思いますけど。 はい。 わかりました。 じゃあちょっと監守が はい。 分かってきたところで次行きたいと思います。今度 最後ですね、自然変換。 はい。 ま、こちらあの権論のですね、 3 つ目のあの重要な概念っていうことですね。こちらは何です?え、ま、大体権論をこう入門される方って あの監守ぐらいまでは結構、 ま、そこそこ頑張っていけるけど、自然変換ぐらいでちょっとこう、ま、あの、なんて言うんですかね?力尽きるっていう人結構多いんですよね。 でも自然変化もそれほど実はあの難しいことじゃないんだけど、ま、一応まず最初フォーマルな その説明をするとね、今度はあのさっき監守っていうのは県と県の関係 だったんですが、今度は 監修監守の関係なんですよ。 つまり最初ので言うとモナ マカロンから右矢印で手巻き寿司クレープがありましたけどこの矢印の そううん と多分別の何かの矢印の関係性です。 そう、そう。なんか関係性が 2 つあった時にその関係性を比較する意味での関係。 はい。なるほど。 だ、もとの関係のまた工事で見たものの関係が監守でしたけど、 この監守自体をまた上から見るのが そうです。 自然変換。 そうです。そうです。 てことなんですね。 まあ、だから語的に言うとね。 はい。 剣っていうのは既でにその中に関係がの束が入ってるわけですね。 そうですね。があってはい。もとものがあってはい。 だから大体件っていうのは関係を表現したものだと思えば監修というのは関係の関係なんですね。 あ、関係の関係ですね。はい。 だけど自然変換は関係の関係の関係なんですよね。 うん。 なるほど。 ていう3段階の関係になって。 ま、ちょっともう少しだから、あの、ちゃんと説明すると、ま、 Cっていう件とDっていう件があって、 こう CからDに2種類のね、 監修、FとGがあるとしましょうと。 はい。 で、その時にこうFとGの間の関係として はい。 あの、ちょっとあの、記号が矢印の記号変わってますけど、ま、これ自然変換って言って工事の関係を表すっていうことを強調するために矢印を少ししてるんですが、 Fっていう監修からG っていう監修への関係として自然変換っていうのが定義されますと。 はい。はい。 それはあの、あんまり細かく説明するとあの、ま、混乱されるかもしれないのですが、 その大体その Fで関係している Aに対して、Fにで関係してるFA っていうのと、Aに対してGで関係してる GAっていう8つの間の社なんですよ。 ていうの集まり。 それはだからか、剣 Dの中でのあの車の集まりなんだけど はい。 うん。だから大体そのFで移した先、 G で映した先っていうのが対応してますよっていうデータを与えること。 [音楽] なるほど があの、ま、自然変換っていうものなんですね。 だからその5というものが、ま、fのその 自然変化だとして、 その5というもののその aっていうものというのは fの中のaからgの中のaにま、FA ですね。FAからGのっていうで、 それ、ま、あの、ま、あの、一応今これすぐにこう、あの、なんて言うんですかね、理解しなくていいんですけど、大体その感じとしては関係、 Fので作られた関係性と Gで作られた関係性が、 あの、また社で繋がるっていう、そういうデータを与えてます。 で、これ、あ、次、それが満たすべき条件として、これ、あの、言葉だけで結構です。自然性条件っていうのがあります。 後でちょっと説明しますけど、 あ、ほ、だから自然変換と言われて。 そうです。そうです。その関係はこう当てずっぽに作られた関係じゃなくってなんか自然は 自然なんだっていう。 その自然ってのはどういう自然ってことでしょうか? うん。あの、およそこう数学らしからぬ言い方なんですけど、 これ自然でしょっていうかいうそういうその自然なんですね。 然にこれ成り立つじゃんていうか。 そうです。その自然でこう考えるのが自然でしょっていう、そういう条件があります。 ほうほ。 え、それが、ま、ちょっと後で説明しますけど、 承知しました。 これ、こ、これ見てるとやっぱなかなか大変ですよね。 これ大変なので、やはりこれも はい。 あの、あ、これがなん、あれですね、先ほどおっしゃっていただいた関係の関係の関係が そうですね。ま、あの、いわゆる自然変換というのを数学のコンテクストで書く時はこう書きますよっていう ことですね。 ええ、 ではこれもですね。 はい。 ハンバーグであの、ま、説明していただきたいと思うんですけども。 さっきライスセットだったんだけど、今このパンセットになってますね。 パンセットになってますね。だから、ま、よくメニューで見てももちろん左側にライスセット、真ん中に、ま、パンセットでサラダセットみたいなありますが、これライスじゃなくてパンセット。 そう。あの、ライスにしますか、パンにしますかってやつですよね、これは。はい。ですね。 で、その時にパンの方を選択された方は、 あの、パンセット監を使ってるんですよ。 はい。なるほど。 そうするとハンバーグたちがごっそり関係ごとごっそり定食の中に移されてでもそれはパンが付いてる定食として映されるっていう。 なるほど。 ま、それだからあのこれによってハンバーグの件から 定食の件に 2つ監ができたわけね。で、この 2つの監守の間を はい。 自然変換で変換しましょうっていうのがこれです。はい。 あの、具体的には何するかって言うと、あの、ライスセット定食のライスに引っ込めてパンを乗せるっていう、 それが自然変換です。 なるほど。 はい。 これも鉄塔鉄あのなんか食べ物で説明。 えっと、このライスをパンに変えたということは これその自然なんですよね。 ま、 自然になってるってことなんですよね。 あの、ライスをパンに変えた途端にね、チーズハンバーグだったやつがディグラスハンバーグになったりします。しないですよね。 ああ、なるほど。 つまりなんか 自然に変えられるってことなんですね。なるほど。 そうです。なんかその言ってみればハンバーグ料理の間の関係性とかそういったものは保ちながら変換されちゃうっていうのが自然変換っていう、ま、その由来なんですよね。あの、これですね。 つまりその和風ハンバーグをライス定食にしたもの はい。 で、同じラフハンバーグをパン、え、定食にしたものってのはこ左側にあります。 ありますね。 で、あの和風煮込みハンバーグ はい。 に関して同じようにライス定食と思ったものとパンセパン定食と思ったものが右側にあります。 はい。 で、両者には横にこう煮込むっていう関係があります。 ある、あるんだけど、その煮込むっていう関係とそれからライスを引っ込めてパンを乗せるっていう関係はあの同じ結果を生むつまりこう、 えっと、左上からまず横に行って煮込んで はい。はい。 で、右下に降りるっていうやっても とはい。 逆に逆にっていうかね、別の方向まず下に行ってから横にやっても同じことでしょ。 はい。結果は一緒になると。 和ハンバーグライセットがその結果和風ハンバーグパンセットになる。 そうです。そうです。そういう意味で、ま、普通に起こり得ることを自然に起こることが自然に変換されるよっていう そのなんか関係性とかそういった ものが保たれながらっていう。 なるほど。 これは先ほどその定義でちょっと少し難しいような形書いてありましたけども、その自然性、自然対象性でしたっけ?えっと、 え、ま、自然、自然変換の自然性というやつですね。 ま、これになってると。 はい。そうですね。 ま、あの、もっと本当に自然変換っていうのは権論において 一応本当は深い概念なんですね。それをあの、ま、簡単とはいえ、あの、こんな感じでこうパッとこう説明しちゃうとちょっと私はあの、両親の過解釈ありますけど、ま、大体、え、大体こんな感じっていうことになりますね。はい、 分かりました。1 個ちょっと戻んですけども、こちらはその矢印下方向にバって書いてありますけども、これはなからなのでその監守っていうものを少し変えてるっていうことなんですね。 はい。 で、上がセット監で、下が監になっていますけど、矢印がそのそれで変わることによってまた右の定食の中の あれが変わってくると。 はい。 だ、注文してからいや、やっぱりあのパンセットにしますっていうのがこれです。 はい。 で、あれはだから1個1 個の単体の定食に対してやってる操作だっていう風に思えるんだけど実はそれはもうこう要するに定食全部に関してごそっとできる 自然な装なんですよね。ていうはい。かなり苦しいですけど 1個基本なのはそのパンライスセット はい。 のものからパンセットへの はい。監守で、 ええ、 それは監守を使えば少し自然変化ではなくてもその監守でも表現できるんじゃないかなってあるんですけど、それは それはね、 え、 だからつまりそれよくある疑問でつまりその自然変換って監で読み替えていいんじゃないですか? つまりそのライス、 え、セットハンバーグの剣っていうの考えて、 パンセットハンバーグの件っていうの考えて、そっから先の監守っていう風に思いましょうっていう。 それ、ま、もうできます。 できるんだけど、あの、ちょっとその辺はね、あの、ニュアンス違ってて、 あの、ハンバーグの件っていうのはハンバーグたちの間のこう関係性っていうかな、つまりハンバーグっていう料理自体が持っている設計図を、ま、表現してるもんだという風に思いましょう。 ま、そういうもんなんですね。 ま、てのは大体そういうなんかこうある種の構造の設計図だっていう風に立ちわれることが多いんです。 はい。 で、え、監守ってのはその設計図に基づ、その設計思想に基づいて具体的なものを作るっていうのが監守なんですよ。従って背後にある設計思想っていうものはそのまま保ちながらも違うものを作ることができ変換するっていうそういう思想なんですよ。 ははは。 それがもしあの単に、 え、監修だけではい。 監修だけでやっちまっ、え、定食ハンバーグの件と、え、パン定食ハンバーグの件で考えちゃうとその設計図ってのは忘れたことになっちゃうんですね。 なるほど。 その背後にある設計図は完全に忘れて単に え、そこだけの関係なってしまうということになっちゃうからうん。ちょっと違うですよ。ニュアンス的には。 あ、いや、よくわかりました。 はい。 なるほど。ま、 そのためにやっぱりこの概念が あるわけですね。 その自然変換と監視とさん検討。 そう、ありがとうございます。はい。なかなか大変ですね。 はい。ここまであの権論の柔概念兼自然変化について はい。 ま、視聴者皆さんも分かってきたかと思うんですけどもじゃこっからですね、まずこれが分かったら その生活や仕事にま、どう応用できるのか、そういうとこについてちょっとまずお伺していきたいなと思います。 でですね、そのあの取り入れるキーワードになるものがこの最大公約数だということで、こちらをちょっと説明いただいてもし はい。はい。や、あのね、これはえっとですね、ま、よく我々その 2つの意見の最大公約素を取るとか はい。 言うじゃないですか。 うん。 だから最大公約数ってすごいいい言葉だなと思うんですけど、で、その実は使われ方っていうのは実は非常に権論的なんだっていう ことをちょっと説明しようと思って、 それが権論だったんですね。 結論だということなんですよ。ま、これ最大公約数ってのは何なのかって言うと、ま、まず公約数じゃなきゃいけない。だからこう AとB っていうその性があったら、あの、ま、 D っていうのが最大公約数だとすると、それはまず公約数じゃなきゃいけないと。 Aの数でもあり、 B の数でもあると。で、そのそういうものの中でその最大じゃなきゃいけないよね。 はい。 で、ここで最大って言ってる意味がこ Bって書いてる条件で、つまり AとBのどんな公約数も実は D の数になってると、その数たちの中で、ま、そのいわゆる割り切れる、割りきれないの関係において最大になってるっていうのが、ま、最大公約数だっていう、ま、こういう風に習ってない。 と思われる人がいるかもしれないんで、そういう人はあの是非本読んで欲しいんですけど、そのこれこれでいいんですよ。 はい。 で、こういう風にこう定義した時にこういう考え方ってよくやってるよねっていうことなんですね。で、それ例えばですね。 はい。 えっと、これでいいましょうか。 はい。 あの、ま、会社の中で社長さんがいて、ま、いくつか部署がありますと。 で、ま、あの、社長さんつよつ強よで、 あの、部署弱、弱わとしましょう。 はい。 で、この場合 はい。 この図だとね、 こう部署と 各部署と社長は直接こうなんかトップダウンで繋がってるんだけど、これ横行の関係ってないみたいな。ま、相談役なんだけど、それもなんかあのやたらと社長に寄り過ぎてるとかじゃなくって はい。できるだけ部署12 に近いだけど、そのそこで 1回こう意見が集約されるみたいな そういう場所だからまさに 約数倍数の関係で言うと 高約数的な 共通の あの役職なんだけど 1番最大この場合だと まあ1番こう下に来てる部書1部書2 に近いっていうそういうものを作りたいっていう風に考えた時にまなんか調整薬っての作りますよねん今の場合 20と36の最大公約数が4なんだけど、 その作り方に、ま、よく似てるわけです。 はい。 で、それはどういう風に作るのかって言うと、部署 1と部署2に社長から 矢印が行く時の こう分岐点のとこなんですよね。ちょうど。 うん。 分岐点のところに調整薬を作るとちょうどうまくいく。 例えば 20と36だと4っていうのがその 数倍数の関係で言うとちょうど分岐してるところなのね。 [音楽] ほほほほ。1 と4の間に2ってのなります。 ありますね。それも両方とも公約数ですね。 公約数なんですけど2はよろしくないのは 2 はもうちょっと下に下がってもまだ共通していけちゃうわけですね。 ああ、つまりその2は うん。 車掌に近いと。 そう、そう。ちょっと車掌に近すぎる。 だ、もうこれ以上も下がれませんっていうところの分岐点のところ。 はい。 うん。ま、あの、だからこう本当に道なんか街道とかでも 街道歩いていてこう分岐点ってあるじゃないですか。あの分岐点のところっていうのがやっぱりなんかそのこうコアになるっていうか重要性が高いかったりするわけですね。ほ うん。その部分にのところにあの、ま、 あの、調整薬を作りましょう、それが最大 公約数的だっていう風に考えるという風に 考えると、ま、あの、最大公約数 を検論の言葉にすることができます。で、 それは直席なんですけど、直席というね、 え、そういうその検論のあの、ま、 ちゃんとしたあの概念があります。はい。 で、今の場合だと、あの、社長と部署 1部署2 の図式の直接を作るとああいうその調整薬っていうのが出てきるっていう。別になんかもう新しいこと言ってるわけじゃないんですよ。これ我々普通に考えてるんです。こういうことって。あの、要するに大体最大公約数的ぐらいのところに何か 1 人をたらいいよなっていう普通に考えますよね。 で、そういうことって例えばそれとあの本当に 20と36 で読んだっていうあの最大公約数が関係してるっていうことを我々普段考えないと思うん。 そうですね。はい。 うん。 だけど実はそれはあの関係してるわけですね。同じ言葉で 権論的には語ることができて なるほど。 ええ。 だから本当に聞的な考え方をすれば本当物だけ囚われてる時とかっていうのはやっぱりその関係性をまず 1個考えてみようっていうところで その関係がどうなってるのかって踏まえた上で全体構的なことが分かってくるっていう そう でそのこと自体はすごく数学的な 概念なんだけどそれはあのすごく我々が普段 あのやっている考え方にすごく近いし 逆な言い方をすると権論の言葉を使えば より日常的な え あの世界にその言葉を応用して、ま、日常世界をね、もっとこう、ま、精密に正確に強力にこう、あの、見ることができるっていう なるほど。 そういうことになりますね。だからね、 だからその社会を見る目を強化できると ええ、そうです。 いうとこに繋がってくるってことなんですね。 はい。え、 まさにその、えっと、もう 1個、 これは、え、社長が はい。 ええ、1 で はい。 女性が4 でここに置けばいいとバランスを通ってますね。 はい。 で、これを うん。 その会社の組織にも 考えを適できるというとこでだんだんは悪乗りしてくるわけですけど、こう 1つの会社を こう件だと思いましょうっていうはい。 だからこうやっぱり1 個の会社の中ではたくさんの 人が 彼らが各人こう矢印で繋がってるわけ。それ矢印は見えないけど繋がってるわけですね。 それが、ま、1 個の件として、ま、会社を見るっていう、 ま、見方なんじゃないかなと思うんですけど、ま、 会社っていうのは1 個単独でその、あの、存在してるんじゃなくってやっぱ取引先があって会社単位でこうネットワークで繋がってますね。 はい。会社ですね。はい。 え、それが、ま、結果あの監守っていうことになるんだけど、こういう感じなわけですね。だ、 Aっていう会社があって、B っていう会社が、ま、あるとはい。 で、ま、あの、Aという会社はその中で 人々が矢印で繋がってるし、Bっていう 会社はまたその中であの矢印で繋がってる わけです。で、それがまたあの矢印の 繋がっている関係 繋がってるっていうそういうことですね。 例えば、えっと、 Bさん、 はい。 A、A会社の、A会社のBさんはB会社の Bダッシュさんに 関係繋がってるとかね。 Cさんは、 えっと、C ダッシュさんに繋がってるんだけど、あの、 E さんは繋がってるなんかあの相棒がいませんよって思うんだけど、実は EさんはC ダッシュさんにつがるんですね。だからC とE さんは実は同じ人、同じカウンターパートを持っている。 こう考えると、例えばその他の組織でなんか組織運営がうまくいってるとかっていう時にこの役職などを見て、あ、こういう関係性でうまくいってるんだったらっていうことで、例えば A株式会社がうまく行ってるとしたらB 株式会社それを、 ま、関係をどういう 移すかってことを考えながら そう やると ええ うまくいきそうですしない部分がもし E さんがものすごいいい仕事してるんだったら 右にももう1回じゃあE さんがいじゃないかとか そうBがうちEさんいな じゃ、みたいな。またですね、この はい。 真ん中の矢印が2種類。そう、そう。2 種類あるかもしれない。だから役職じゃなくって こう色とかね。ま、役職と色だとちょっと微妙に違ってる可能性があるからそれでカウンターパートを作るとか言うとまた違う 監守になるかもしれませんよね。その関係の関係の関係として はい。 あの、要するに役職カウンターパートっていう関係と色々カウンターパートっていう関係の間に破変感を入れてるっていう。普段あんまりこういうことって 無意識に考えると思うんですよ。やっぱりこう会社との付き合いをする。 そうですね。考えてますね。多分相手の立場とかどんなぐらいなんだろうとこっちはじゃあその例えば解食とかでもええ、 先法がその部直になっちも部長行った方がいいか。そう、 その時やちょっと待って。 それ役職じゃなくていいんじゃないとかっていうなるとバッとこうあの変換が切り替わるとかね。 そういうことって普段やってんだけど うん。 あんまり言葉にできないですよね。 言葉にしないですね。それを 言葉にしたことないですね。それを何でやってるのかっていうか。 ええ、 でもこの権論の言葉をマスターすれば そういう言葉で喋れるようになるという。は い。あ、 そうするとみんながその精密な関係の関係の関係の話を今してるんだなみたいなそういうコミュニケーションが取れるようになるかもみたいな。 なるほど。がちょっと高くなるというか。 ええ、そうですね。そうするとやっぱりこう仕事もはどるんじゃないですかね。 あの、はい、あの、適当なこと言ってます。 でもすごくありそうな気がしました。しました。 はい。じゃ、私たちは普段多分考えていること うん。 なんですけど、それまさに言語化できるのが権論だっていう ところで多分だから皆さんが権論を うん。 分かっていればその新たな言語と言いますかでさらにその関係の関係の関係まで議論できるようになっていくことなんですね。 そうですね。ええ。 ま、だから数学でも、 ま、全然私数学の話してないような感じ。 そうですね。今日はあの、ずっと料理の話をしてる。 料理の話ばっかりしてますけども、実はでも数学の話を実は僕はしてるつもりで、 あの数学の世界でもこの剣っていうınıとか監視とか自然変換っていうのはあの数学の中でもそれまでになかった非常に豊かなこう表現ツールを与えたわけですね。 で、実際、あの、ま、今日先ほど、あの、お見せしたように、その、ま、先ほどはそのカルボナーラのレシピっていうのでお見せしたんですけど、 あの、そう、あの考え方っていうのは数学の様々な 例えば家程とかはい。 あるいは、ま、漁子力学のその漁子とかね、 そういったものにも応用されているし、 もう既でに応用されているんです。 そうです。そうです。 最近だと、あの、えっと、例えば、あの、ベーズ水定とかあいうのをこのストリング図寿式で書くっていうね。そうす、こうイン果水論とかそういったものもこうストリング水論で書けるんですね。 はい。 というような、そういうことも実はできるし、今までになかったようなその、それまでは本当に数式を書いて左辺を右辺にこうあの変形していくみたいなそういうものばっかりだったんだけどなんとなくこう楽しくなるような料理のレシピみたいな図を書いてあの数字権がかけるようになるっていう新しい表現形態を与えてるわけですね。 で、その単にその表現ツールとしてだけじゃなくって、そっからまた新たなそのなんですかね、考え方とか視点とか そういったものもこう与えてくれるわけですよ。 で、そうしたらもう数学だけじゃなくって 社会で使ったら良くないっていう ことですね。 うん。 ま、実際権論は例えばそのAI の最新研究であったりだとか、ま、トポロジーとかそういったとこでも使われてると思うんですけども、ま、今後はじゃあ社会とかそういったとこにも使れていくんじゃないか。 あの、ま、今トポロジーとかなんかおっしゃったトポロジーはそのいわゆる期科学 台数的期科学っていうのは本当に権論がそのそっから発生した土上なんですね。 むしろそこが そう、そこがオリジナルですよ。 で、今AI と申し、ま、残念ながらっていうか、最近の AIの 研究の流に権論があるかっていうと、それは多分ないんですね。 その権論 って少しだからあの高級すぎてというか理論的すぎてあんまり使われてないっていう今はまだそうかもしれないけどその理論的なところであの AI とかを支えるっていうことは十分あり得ます。それからあと社会科学、事務科学 の不世界ではま、何しろねその なんですかね。その関係性を うん。 記述する言葉例えばですよ。 その関係後のネットワークがあの詳細に記述されるとね、 もともがいつ同じと見なせるかとかっていったことが実は関わってくるんですね。 ほほほほ。 例えばAとB の間にAからBにも関係があり、同様に BからAにも関係があると はい。 いう時にこう両方お互い関係し合ってるという意味では非常に似てるっていう見合わせる。 ある種こうそれが強いその関係が強くなってくると 同じと見なしても 同じと見なしても良いっていううん。うん。ま、数学ていうと同計っていう言葉があるんですけどその同じさみたいな はい。 あの、そういった概念を深く考えるモデルを与えるんですよね。で、だから例えば哲学とかだとそういう はい。 え、まさに1 つの哲学のやり方っていうのはその世界を見る時に その何は同じと見なして何は同じと見なさないかみたいなこと自体をその学ぶというか そういうものを研究するってのは1 つの哲学的な あの社会の見方だと思うんですね。 で、実際そういうことを、あの、認知科学とかの視点からやってる人はいます。 え、認知科学とか哲学の世界であの権論を使って うん。 え、ま、研究してる人で、 えっと、書いた本が実際あるんですけど、 ち選手で はい。はい。 えっと、現実とは何かっていう、 現実とは何かはい。 で、ちなみにその最後先生っていうのは全大学の先生なんですけど。 あ、そうなんですね。一緒ですね。 はい。 というわけで、まあ、なんかすごくその、あの、検論はこう社会に、ま、めちゃめちゃ応用される可能性を [音楽] 秘めている。 秘めている数学だけじゃないってことですね。ま、最近だと応権論っていう言葉も 出てきていてはい。 そのうちだからあのストリング図式とかで小説書くとかね。 はい。こんなま、今出てるからこう読めるとかね。 これで読めるとあれだからこう同時進行でいろんなこと見えるので はい。 うん。 うん。だからこう、あの、推理説とかいいんじゃないかと思うんですよね。 そんな未来があるかもしれないですね。確かに。え え、 本日、あの、権論について加藤先生にお伺いしました。ま、本当に権論あの数学じゃなくて本当にま、社会に実装してきてるんだなっても分かりましたし、あの、今日もカルボランナー作り方とかですね、全部論でで、まさにこれが数式だということで、ま、こういった方ですね、本当にいろんなものとか駐車な概念から議論できると本当に社会を見る目が強化されそうだなという風に、え、思いました。 あの、今日はちょっと料理の話ばっかりだったかもしれないんですけども、ちゃんとこの 著書の中にはですね、しっかりとした、あの、あの、権論をどう記述していくかとか、どう合成できるのかとかですね、最後先 1 回だけありました、直接のような話とかも載っていますので、是非皆さん手に取っていただければと思います。え、今日は数学者の加藤ふ原先生にお話をお伺いしました。え、今後も様々なテーマを掘り下げていきますので、え、是非チャンネル登録と高評価よろしくお願いいたします。今日は本当にありがとうございました。 ありがとうございました。 [音楽]

https://youtube.com/@tbs_bloomberg
👆チャンネル登録・高評価をよろしくお願いします

「最中とマカロン」と「手巻き寿司とクレープ」の関係性は似ている。こうした“関係の関係”や“関係の関係の関係”を記述するのが数学「圏論（けんろん）」です。
一見、難解な数学「圏論」が、いま数学界を飛び出し、私たちの日常やビジネスの「見る目」を強化するツールとして注目されています。
数学者の加藤文元さんが「圏論とは何か？」という根本から、「関係の関係の関係」を語る言葉までを、ファミリーレストランのハンバーグメニューや、会社の組織図といった身近な例えで徹底解説。ほぼハンバーグで圏論を語ります。

＜書籍＞　
『はじめての圏論　ブンゲン先生の現代数学入門 (ブルーバックス)』加藤文元／講談社
https://amzn.to/3WP6WTr
『〈現実〉とは何か』西郷 甲矢人,田口 茂／筑摩書房
https://amzn.to/4o12w7Q
※URLはAmazonアソシエイトを利用しています

＜出演＞
▼加藤文元
数学者　ZEN大学教授
1968年、宮城県生まれ。東京工業大学(現・東京科学大学)名誉教授、株式会社SCIENTA・NOVA代表取締役、ZEN数学センター(ZMC)所長、NPO法人数理の翼顧問。
1997年1月に京都大学で博士（理学）を取得し、九州大学助手、京都大学准教授、熊本大学教授、東京工業大学教授を歴任。専門は代数幾何学および数論幾何学、特にリジッド幾何学（非アルキメデス的幾何学）で、長年に渡りその基礎付けの仕事に携わる。数学史や数学者の思想・生涯、さらには数学の考え方などを題材とした一般の読者向けの数学の啓蒙書も多数出版。趣味はピアノと合唱で、京大の学生時代にはプロの指揮者に師事して斎藤流の指揮法を学んでいたほどの音楽好き。

▼鈴木有
TBS CROSS DIG with Bloomberg サイエンスエディター
物理学科出身。前職はNHKで初任地は鹿児島。記者として、宇宙、基礎科学、文化、ITなどを幅広く取材。2025年7月にTBSテレビ入社、TBS CROSS DIG with Bloombergに加わる。
科学の専門家を招いた番組「1on1」や「ULTRA SCIENCE」、医療の「1on1 Health」、教育系シリーズ「まないく」を主に担当。4児の父。
Xアカウント @aru4649

▼チャプター
00:00　番組開始
00:56　社会の見る目を強化する数学『圏論』
04:26　「圏論」とは何か
10:05　圏論の神髄 圏・関手・自然変換
31:14　圏論が拓く世界の新しい景色
32:51　調整役と最大公約数
37:06　自然変換で会社組織を理解する
43:57　「圏論」で小説だって書ける?!

＜収録日＞
2025年10月8日

※一時、「関手」の説明の部分でスライドが間違っており、修正対応をいたしました。

▼TBS CROSS DIG with Bloomberg
https://newsdig.tbs.co.jp/list/withbloomberg

▼公式Xアカウント
https://x.com/tbs_bloomberg

#tbs #crossdig #tcdb